
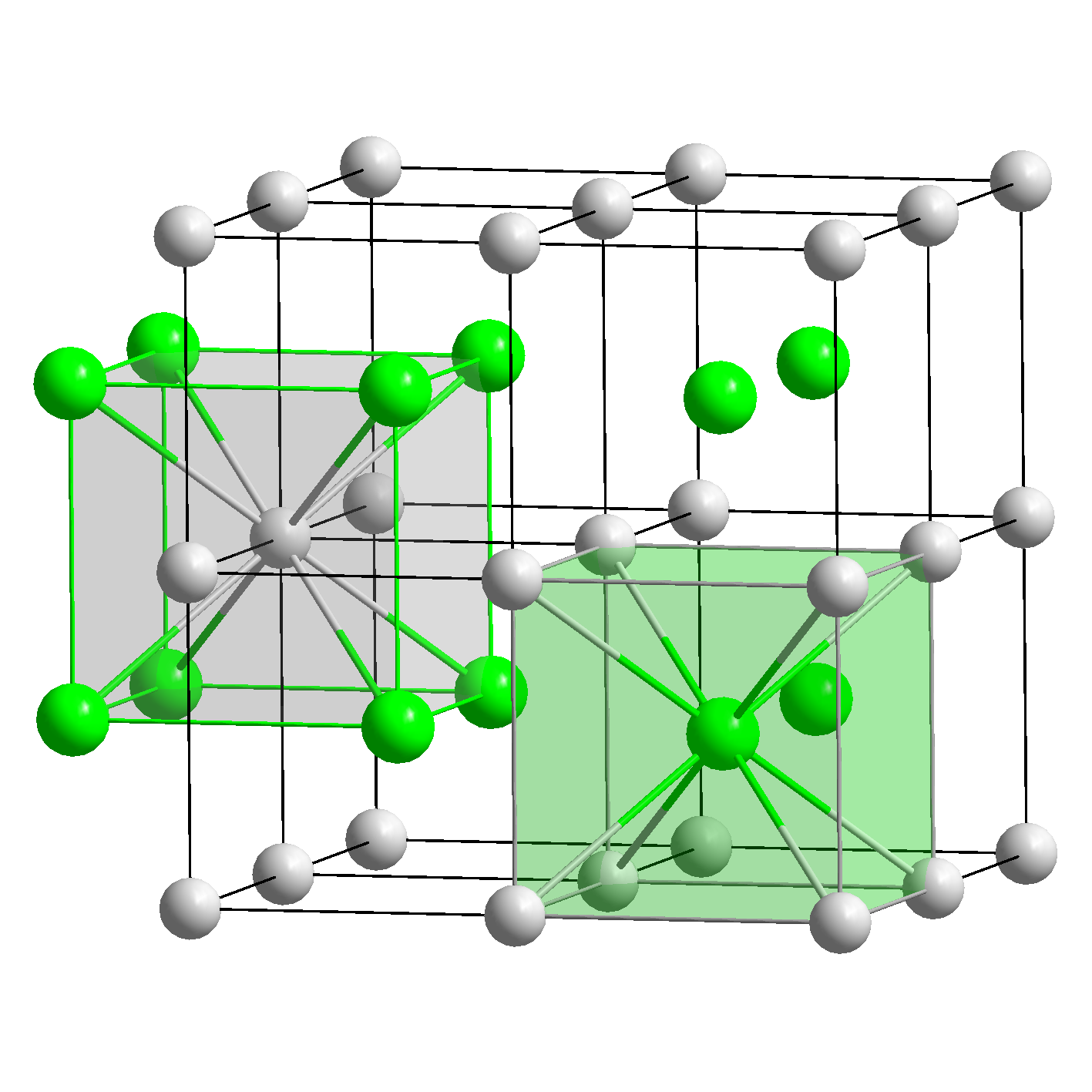
If you connect the six centers of the surrounding spheres you generate the octahedron.įace-centered cubic (fcc) lattice structures provide a framework for octahedral holes. The polyhedron can be constructed by one sphere surrounded by 6 equal spheres (Figure 7A). The octahedron is a polyhedron made from 8 regular triangles. As you may have noticed the cation occupying the center of the cube is smaller than the anions on the corners of the cube. In a body-centeredcubic structure all the atoms in the unit cell are identical (See section on Body-centered Cubic Cell). Cesium chloride does not pack in a body-centered cubic structure. It is convenient at this point to clarify the misconception concerning CsClarrangement. Each unit cell has one cesium ion and one chloride ion. Alternatively, it can be viewed as a chloride anion surrounded by 8 cesium cations. The smaller cesium cation sits in the hole surrounded by 8 chloride ions. This lattice framework is arrange by the chloride ions forming a cubic structure. An example of this packing is CsCl (See the CsCl file left Cl - yellow, Cs + green). As you can see in Figure 6 the cation can sit in the hole where 8 anions pack. Let's start with anions packing in simple cubic cells. Packing arrangements like simple cubic (sc), cubic close-packed (ccp), hexagonal close-packed (hcp) are examples of structures which minimize same charge interactions. Usually the larger anions make up the framework of the crystal lattice and the smaller cations then occupy the spaces or holes left between the framework of anions. Ionic compounds are made up of anions and cations. The result is an organized three-dimensional arrangement of ions and counter-ions. Ions of opposite charge can occupy these spaces. Compounds like salts fulfill this requirement. It is crucial that we consider that there are holes within these lattices (rotate the 3D fcc model) which can be filled with smaller ions or particles - we will see this later - thus increasing packaging efficiency. Some examples of fcc arrangements are: aluminum, copper and buckminsterfullerenes C 60 (bucky balls). (See figure for calculations)įace-centered cubic cells have a 74.0% packaging efficiency for spheres or ions of equal diameter. This gives us a total of 4.Ĭalculation of the edge value is quite straightforward. The total number of particles within the lattice can be calculated as follows: 8 particles on the lattice corners (1 particle),6 particles with half of their volumes within the lattice (6 particles* 1/2 volume = 3 particles). The two-dimensional layer representation shows that there are six particles which have half of their volumes within the lattice. It has a particle in the middle of each of the six faces of the cube. Illustrated left is the face-centered cubic (fcc) unit cell. The virus that causesfoot and mouth disease in animals also exhibits bcc crystal arrangements. Potassium (alkali metal) and iron are examples of metals that arrange themselves in bcc.
The ratio of the volumes where all particlesare equal gives us a 68.0%. But we should realize that the lattice volume has increased accordingly. We might expect to have a greater packaging efficiency because there are more particles within the lattice compared to a simple cubic cell. The number of particles in a bcc unit cell is 2, determined as follows: 8 spheres on the lattice corners each with an eighth oftheir volume within the cell (1 particle) and one sphere completely embedded in the lattice. To determine the edge value we must rely on the diagonal of the two opposite corners of the unit cell. So in this case the edge is greater than two atomic radii of the lattice corners. The bcc has 3 layers (along the z-axis),which would look like this: Another way of looking at the layout is using 2-dimensional layer diagrams.
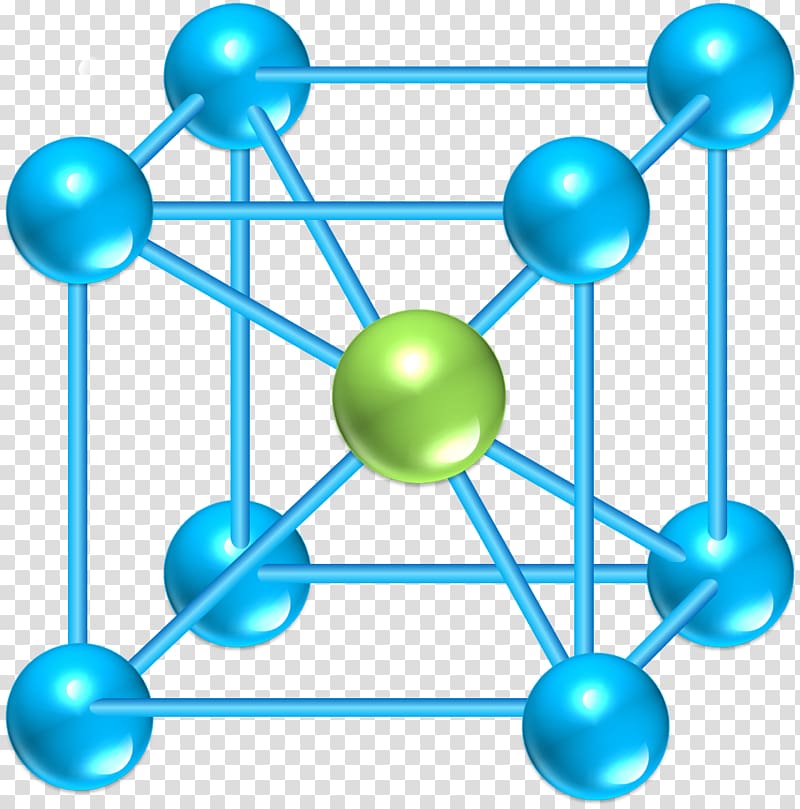
As the name suggests it contains an ion or atom in the center of the cube.If all the spheres have the same radius, like in metals, then the spheres centered on the lattice points do not make contact with each other. Rotate the body-centered cubic (bcc) unit cell. One important question should be asked: what is the efficiency of packing same size atoms in simple cubes? Because there are a total of eight one eighth volume spheres in the cell the simple cubic unit contains one net particle. But the unit cell only contains, on the lattice points, an eighth of the volume of the sphere (ion or atoms). The volume of the unit cell then is the edge cubed (edge 3). Observe that in the simple cubic cell the edge equals two atomic radii. As you rotate the spacefill model around you will notice that all the spheres (ions or atoms) are in contact with each other.


 0 kommentar(er)
0 kommentar(er)
